Геометрия |
Методическая копилка |
Прямые и плоскости в пространстве |
|
Занятие 1 . |
Взаимное расположение двух прямых в пространстве. |
Занятие 2 |
Признак параллельности прямой и плоскости. |
Занятие 3 |
Взаимное расположение двух плоскостей. |
Занятие 4 |
Теорема о трёх перпендикулярах. |
Занятие 5 |
Двугранный угол. Линейный угол двугранного угла. |
Многогранники |
|
Занятие 6 |
Понятие о многограннике. Правильные многогранники. |
Занятие 7 |
Прямая и правильная призма. Параллелепипед. |
Занятие 8 |
Пирамида. Усечённая пирамида. |
Занятие 9 |
Решение задач по теме "Многогранники". |
Тела и поверхности вращения |
|
Занятие 10 |
Тела и поверхности вращения |
Занятие 11 |
Цилиндр. Конус. |
Занятие 12 |
Сфера. Шар. |
Объемы тел и площади их поверхности |
|
Занятие 13 |
Объём параллелепипеда, призмы, цилиндра, пирамиды и конуса. |
Занятие 14 |
Площади поверхностей призмы, пирамиды, цилиндра и конуса. |
Занятие 15 |
Объём шара и его частей. Площадь сферы. |
Координаты и векторы. |
|
Занятие 16 |
Координаты вектора. Скалярное произведение векторов. |
Занятие 17 |
Угол между векторами. |
Занятие 18 |
Векторное произведение векторов. |
Признак перпендикулярности прямой и плоскости. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим
через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости,
не являющийся перпендикуляром к плоскости.
Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
1) Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
2) Две прямые, перпендикулярные одной и той же плоскости, параллельны.
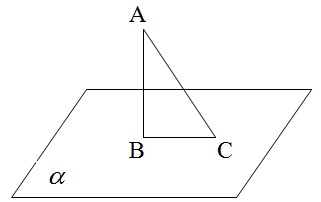
АВ - перпендикуляр
АС - наклонная
ВС - проекция наклонной
В - основание перпендикуляра
С - основание наклонной
Теорема 2. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.